| Настя
Offline
| Дата: Воскресенье, 11.12.2011, 12:07 | Сообщение # 1
|

Модераторы
Сообщений: 157
| Деформацию металла можно определить с помощью следующих коэффициентов: высотного обжатия, вытяжки и уширения. Эти коэффициенты можно определять как за один проход – частные коэффициенты, так и за все проходы – суммарные.
Частные коэффициенты. Если обжатие по ширине полосы распределяется равномерно, то оно определяется по уравнению
Δh = h0 – h1,
Если же оно распределяется неравномерно, то уравнение имеет вид:
Δh = h0ср – h1ср,
где h0ср – средняя высота металла до прокатки;
h1ср – средняя высота металла после прокатки.
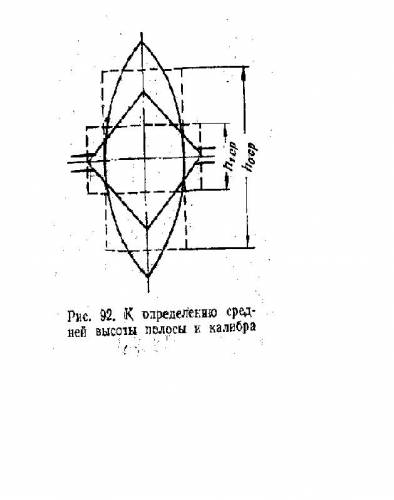
Для определения средней высоты полосы (калибра) ее необходимо заменить равновеликой по площади прямоугольной полосой, имеющей ту же ширину (рис.):
hср = F / b,
где F – площадь поперечного сечения полосы;
b – ширина полосы;
hср – средняя высота полосы.
Относительное обжатие определяет уменьшение площади поперечного сечения металла, выраженное в процентах:
δ = (F0 – F1) х 100%,
F0
где δ – относительное обжатие;
F0 - площадь поперечного сечения металла до прокатки;
F1 - площадь поперечного сечения металла после прокатки.
Вытяжка определяется как отношение длины полосы после прокатки к длине полосы до прокатки или отношение площади поперечного сечения полосы до прокатки к площади поперечного сечения после прокатки:
λ = l1 / l0 = F0 / F1 .
Уширение металла при прокатке можно определить как разность ширины полосы после и до прокатки.
Уширение зависит от ряда факторов, в том числе от обжатия, коэффициента трения, температуры прокатываемого металла, скорости деформации, свойств металла, формы калибра и др.
Как было указано, уширение при фасонной прокатке не свободное. Кроме сил внешнего трения, на уширение влияет боковое давление стенок калибра, уменьшая его. В отдельных случаях калибр может оказывать разгонное действие на металл и уширение в этом случае будет вынужденным.
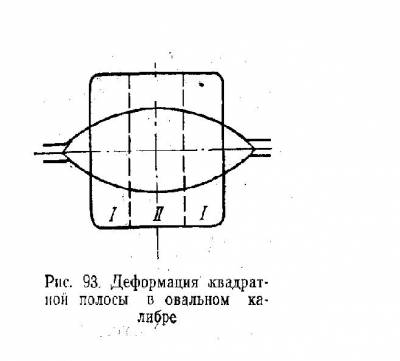
В других случаях неравномерной деформации будет происходить вынужденная утяжка. Рассмотрим, для примера, прокатку квадратной полосы в овальном калибре (рис.).
Разобьем по ширине металл на три части. Как видно на рисунке, крайние части металла имеют большее обжатие, чем средняя, и, следовательно, стремятся получить большую вытяжку. Вытяжке крайних частей будет препятствовать средняя – сдерживать их, и таким образом крайние части металла получат вынужденное уширение. Этим можно объяснить большое уширение при прокатке квадратной полосы в овальном калибре.
Следует отметить, что при плоской прокатке уширение пропорционально смещенному объему в направлении ширины, так как щель между валками плоская и толщина выходящего из валков металла по всей ширине полосы одинаковая. В то же время в сортовой прокатке даже при небольшом смещенном объеме в направлении ширины абсолютное уширение может оказаться значительным, так как металл в поперечном направлении течет в суживающуюся щель. По такой причине при сортовой прокатке даже значительное уширение не оказывает столь большого влияния на вытяжку, как при плоской.
Правильное определение уширения металла имеет большое значение, так как от правильности расчета уширения зависит правильность заполнения калибра металлом. Неправильный расчет уширения неизбежно приведет к неполному заполнению или переполнению калибра. И то и другое крайне нежелательно, так как при неполном заполнении калибра получается неправильная форма изделия в отделочном калибре, а в промежуточном калибре – неустойчивый процесс прокатки. При переполнении калибров на поверхности образуются заусенцы, которые при дальнейшей прокатке приведут к браку.
Если для расчетов уширения при плоской прокатке имеется много формул, дающих удовлетворительные результаты, то для подсчета уширения при сортовой прокатке таких формул мало.
Суммарные коэффициенты. Суммарная вытяжка определяется как произведение вытяжек по проходам:
λ = λ1λ2λ3…λn.
Если вытяжки по проходам равны или делается допущение о равенстве их средней величины λср, то уравнение для определения суммарной вытяжки примет вид:
λΣ = λnср,
где n – число проходов.
Из этого уравнения можно определить число проходов:
n = lg λΣ / lg λср.
Суммарное обжатие можно выразить уравнением
δΣ = F0 - Fn х 100% .
F0
|
| |
| |